On Structural Criticality:
Atemporal Topological Discrimination of the
Riemann Hypothesis

Keunsoo Yoon
Independent Research Group (Seoul, Republic of Korea)
austiny@gatech.edu, austiny@snu.ac.kr

Jan 9, 2026

Keywords: Atemporal Computation; Changbal Jump Machine (CJM); O(J); Structural Equilibrium; Riemann Hypothesis; Trinity Resonance; P vs NP; NP Problem; Time Crystal; allthingsareP; =;

1 Introduction

The Riemann Hypothesis (RH) is a central conjecture of analytic number theory asserting that all nontrivial zeros of the Riemann zeta function lie on the critical line \(\sigma =\tfrac 12\), as proposed by Riemann in 1859 [2]. Despite major advances in asymptotic analysis [3] and extensive numerical verification [4], the hypothesis remains unresolved. This persistence suggests that the difficulty of RH may arise not only from technical barriers, but also from the predominantly time-dependent formalism in which the problem has traditionally been framed [5]. The possibility that RH admits a spectral or physical interpretation has long been explored, as reviewed by Schumayer and Hutchinson [6], including the Hilbert–Pólya conjecture, which postulates a correspondence between nontrivial zeros and the spectrum of a self-adjoint operator.

The essence of the Riemann Hypothesis lies not in the numerical values of individual zeros, but in the topologically locked-in stability of the zero set as a whole. Analogous to the state description of a time crystal, where structural order persists independently of temporal relaxation, the nontrivial zeros appear embedded along the \(\sigma =\tfrac 12\) ridge as a collective manifestation of atemporal structural equilibrium. From this viewpoint, the critical line represents not merely an analytic locus, but a structurally stabilized configuration whose coherence is maintained independently of iterative temporal processes.

In this work, we pursue a different approach by repositioning RH within the atemporal complexity class \(O(J)\) and the Changbal Jump Machine (CJM) paradigm [1]. This perspective originates from earlier investigations of the P versus NP problem, where solvability was reformulated through the Changbal Atemporal Equation, \(P \equiv NP^{\mathcal {J}}\), collapsing solution and verification under non-temporal structural discrimination. Rather than treating RH as a conjecture to be resolved solely by analytic proof, we examine whether it can be formulated as a physically discriminable structure. Within this framework, resolution proceeds through instantaneous structural admissibility rather than stepwise computation, with coherence evaluated via phase alignment analogous to physical phase-transition phenomena [9]. The aim of this paper is modest: we do not claim a proof of RH, but investigate whether it can be embedded into an \(O(J)\) state space and examined in principle through CJM-inspired discrimination, illustrated via software simulations of \(\zeta (\tfrac 12+it)\) based on classical decision-theoretic formulations [8].

2 Structural Foundations of the Riemann Hypothesis

This section reframes the Riemann Hypothesis (RH) as a problem of atemporal structural admissibility rather than asymptotic verification in the classical analytic sense [7]. In this view, nontrivial zeros are not isolated decisive events but recurring structural features, and the persistence of coherent behavior near \(\sigma =\tfrac {1}{2}\) (Fig. 1) motivates interpreting the critical line as a phase-stable structural region.

2.1 Phase Stability and Structural Discrimination

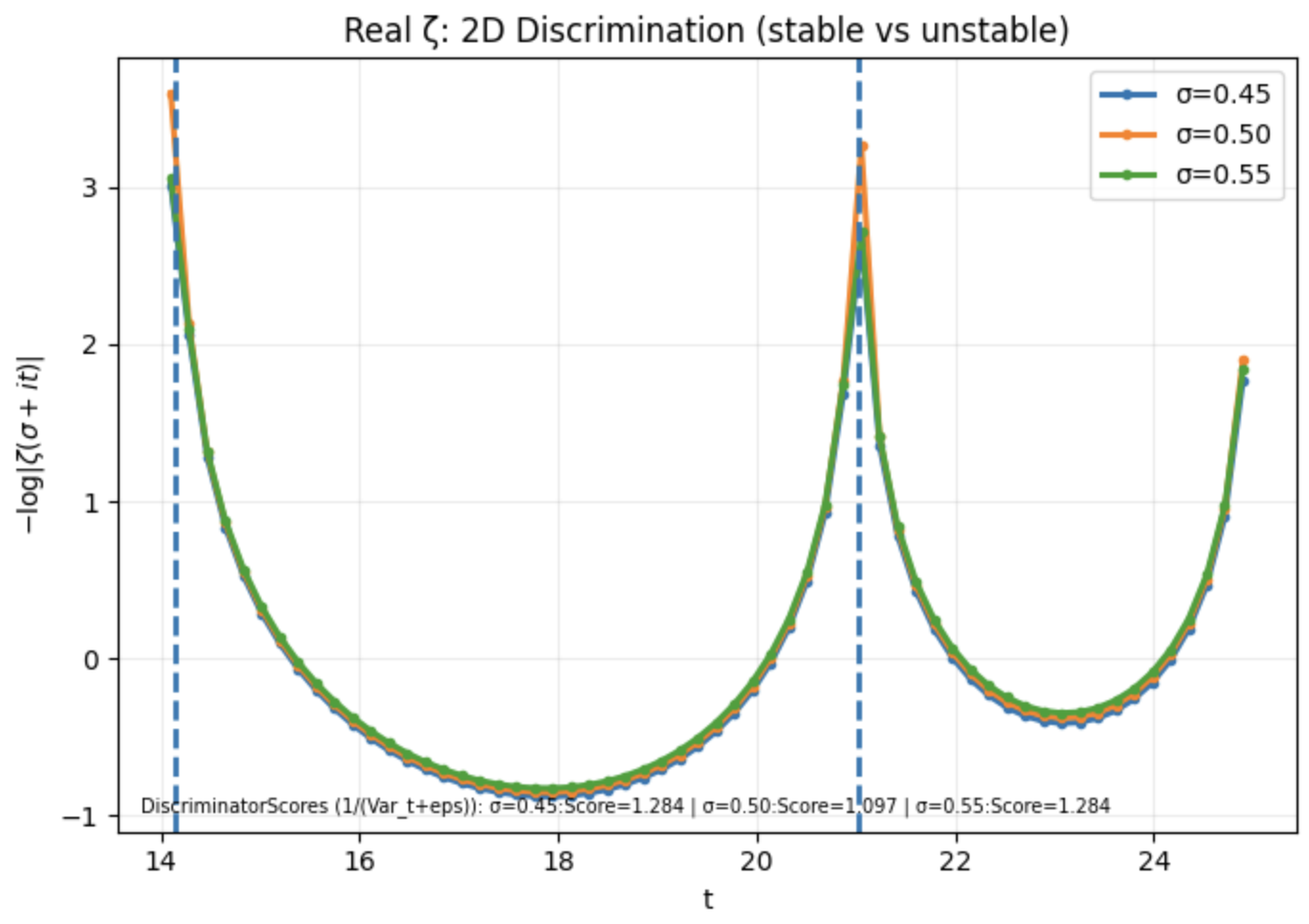
Conventional approaches to RH operate within a temporal paradigm of successive approximation. In contrast, the CJM/\(O(J)\) perspective replaces iterative accumulation with instantaneous structural discrimination, consistent with critical phenomena in complex systems [9]. From this viewpoint, the critical line \(\sigma = \tfrac {1}{2}\) emerges as a privileged manifold along which oscillatory components align coherently.

To formalize this intuition, we introduce a structural coherence probe \(\Psi (\sigma , t)\) defined by a finite Dirichlet-type aggregation:

Although \(\Psi \) does not constitute an analytic continuation of the zeta function, it serves as a structural diagnostic. Numerically, it reveals the critical line as a resonance-compatible ridge [3], while deviations in \(\sigma \) introduce intrinsic decoherence, rendering off-critical configurations structurally unstable.

2.2 Nontrivial Zeros as Resonance Equilibria

Within this structural interpretation, nontrivial zeros are reinterpreted as collective resonance equilibria arising from logarithmic frequency alignment. This view remains consistent with classical analytic theory and extensive numerical evidence [4]. The appearance of zeros reflects an atemporal balance in which phase interference becomes structurally admissible.

Importantly, this interpretation emphasizes exclusivity: coherent realization occurs only along the \(\sigma = \tfrac {1}{2}\) manifold. The Riemann Hypothesis may therefore be restated as a claim of frequency stability, asserting that extremal phase coherence is attainable exclusively on the critical line within the \(O(J)\) state space.

2.3 From Analytic Structure to
Physical Admissibility

The structural reformulation presented above prepares the ground for a transition from purely mathematical analysis to physical interpretation [1]. By treating RH as a problem of structural stability rather than symbolic derivation, the hypothesis becomes amenable to discrimination-based evaluation, opening a pathway toward physically realizable testing paradigms.

3 CJM-Based Discrimination of the Riemann Hypothesis

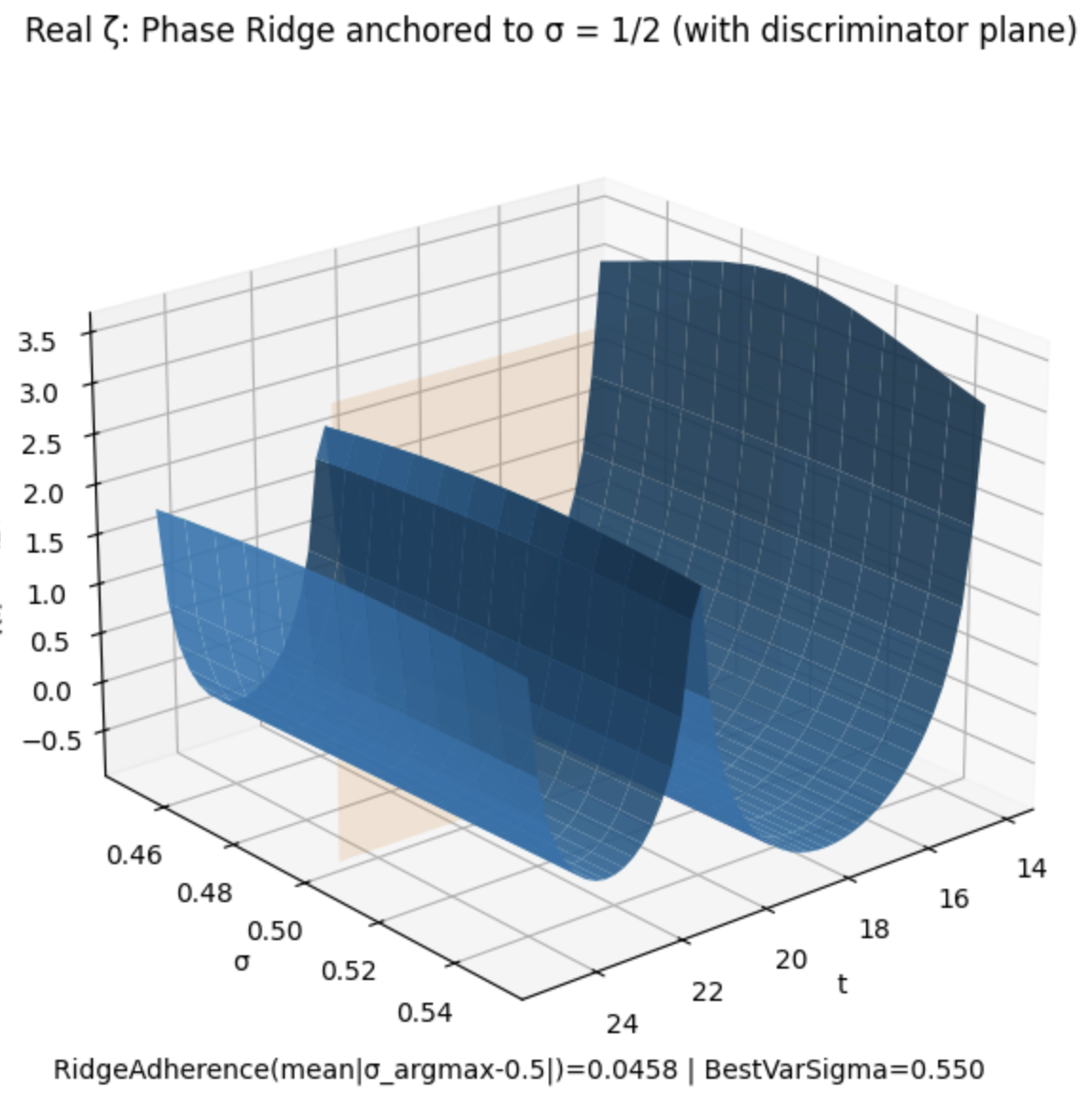
This section provides a self-contained summary of the Changbal Jump Machine (CJM) framework and demonstrates how it can be applied to the Riemann Hypothesis (RH) as a problem of structural discrimination. While the CJM paradigm was introduced in prior work [1], the present exposition is designed to be readable without requiring familiarity with earlier papers, and its interpretation is further supported by the phase-stability landscape shown in Fig. 2, where coherent ridge structures persist near the critical line. The emphasis here is not on proof construction, but on how RH may be interpreted as a physically discriminable hypothesis under an atemporal computational lens.

3.1 Structural Encoding into Boolean Constraint Space

The CJM framework begins by translating analytic or mathematical structures into a constraint language suitable for physical discrimination. This translation does not claim logical equivalence between domains; rather, it provides a common structural interface.

In the case of RH, local phase-alignment conditions of the Riemann zeta function are abstracted into finite consistency constraints. Each local admissibility condition is encoded as a Boolean clause \(C_k\), yielding a conjunctive normal form (CNF) representation:

This construction does not reduce RH to 3SAT in the logical sense. Instead, it embeds the hypothesis into a standardized constraint space through which structural coherence can be assessed [8]. The role of Boolean encoding here is instrumental: it enables diverse problem domains to be expressed within a unified discrimination framework governed by structural compatibility rather than symbolic derivation.

3.2 Atemporal Discrimination via CJM Dynamics

Classical computation evaluates such constraint systems through temporal enumeration or stepwise verification [8]. In contrast, CJM operates in an atemporal regime. Computation is reinterpreted as a single structural resolution event governed by the Jump operator \(J\), which collapses an encoded configuration into a phase-stable outcome if such an outcome exists [1].

Operationally, CJM follows a six-step pipeline: structural normalization of the problem, constraint abstraction, preprocessing-based geometric conditioning, resonant synthesis, atemporal evaluation under \(O(J)\) dynamics, and final physical readout. These steps do not constitute an algorithmic sequence in the traditional sense; rather, they prepare the structure for a non-iterative resolution in which incompatible configurations fail to stabilize.

Within this framework, CJM does not function as a proof oracle. It does not generate derivations or certificates. Instead, it acts as a physical discriminator of coherence: solvability is inferred from the emergence of a stable resonant configuration, while non-solvability manifests as persistent instability or decoherence [9]. Time is not the resource consumed; structural compatibility is the decisive criterion.

3.3 Structural Singularity and the Limits of Software Emulation

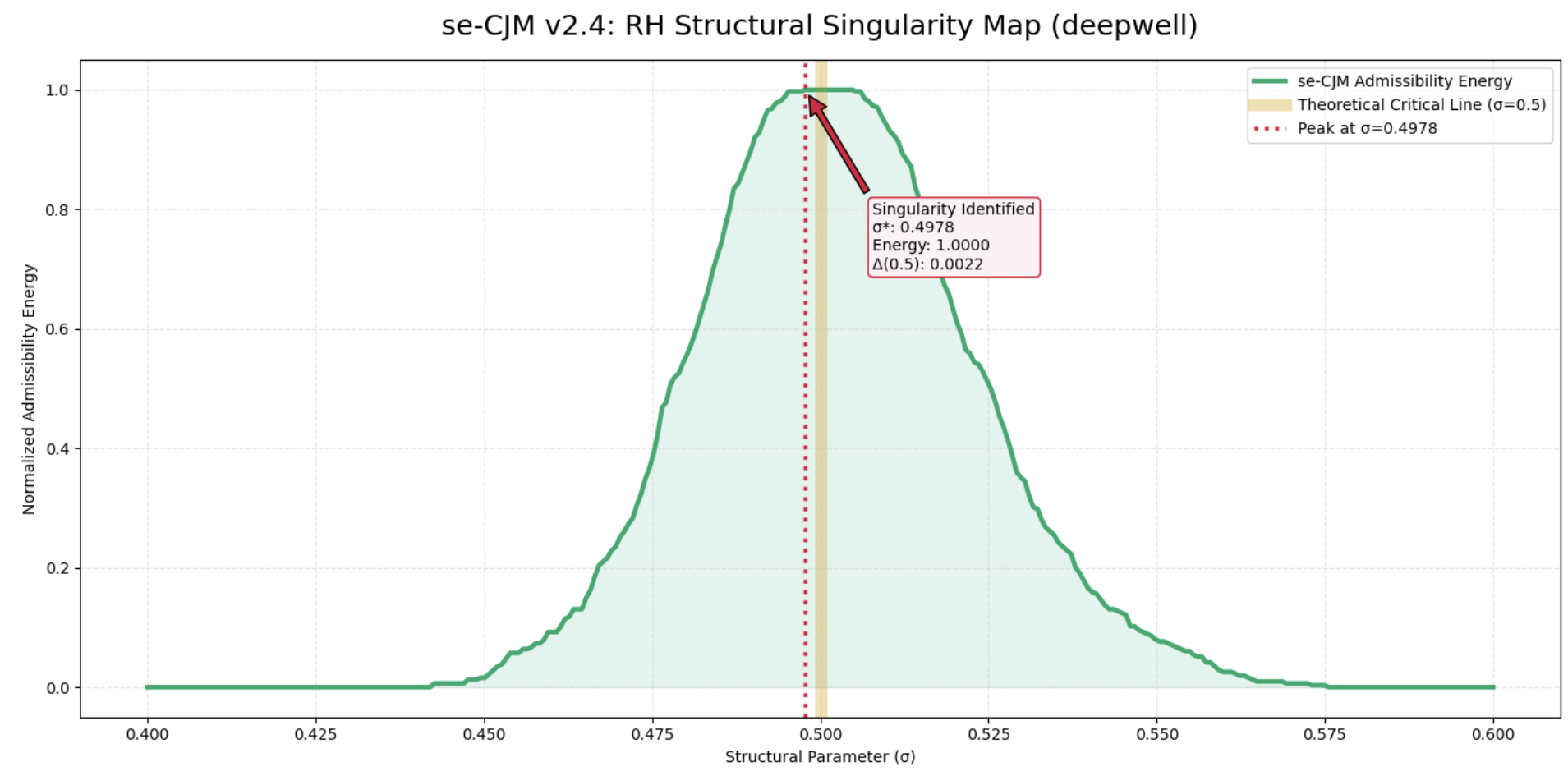
Figure 3 presents a structural singularity map obtained via a software-emulated Changbal Jump Machine (se-CJM), revealing a single dominant admissibility peak sharply localized near the critical line \(\sigma =\tfrac {1}{2}\). Within the CJM framework, the discriminative signal is not the exact numerical position of this peak, but the existence of a unique global structural maximum accompanied by rapid decay away from the critical region, indicating a phase-stable admissible configuration [6].

The persistent numerical tension between the detected peak and the theoretical critical line reflects the inherent limitations of software emulation, including discrete sampling and numerical approximation, and should therefore be interpreted as evidence of organic structural emergence rather than analytical enforcement. In this sense, the Riemann Hypothesis is reframed as a claim about the uniqueness of an admissible structural region, not a pointwise equality condition [5].

However, because the se-CJM operates as a simulator rather than a measuring instrument, it cannot realize continuous, atemporal resonance directly. The structural singularity identified in Fig. 3 thus serves not as a conclusion, but as a precise target for structural locking achievable only through physical discrimination, motivating the construction of a physical Changbal Jump Machine as a necessary next step [1].

4 Conclusion

This work does not aim to prove or formally resolve the Riemann Hypothesis (RH) within the traditional analytic framework. Instead, it advances a shift in perspective: from viewing RH as an exclusively symbolic conjecture to interpreting it as a question of physical realizability and structural stability within an atemporal computational setting. By embedding RH into the \(O(J)\) state space and evaluating it through the Changbal Jump Machine (CJM), the hypothesis is repositioned from the domain of formal derivation to that of physical discrimination.

Within this framework, the critical line \(\sigma =\tfrac 12\) is interpreted as a structurally stable region admitting coherent resonant configurations, while nontrivial zeros are viewed as equilibrium states arising from collective phase alignment rather than isolated analytic artifacts. This interpretation highlights the role of global structural coherence in determining admissibility, consistent with emergent behavior observed in complex physical systems [9]. In this sense, the zero distribution may be understood as exhibiting a form of time-crystalline order, where stability persists independently of temporal relaxation.

A central implication is that RH may be formulated as a physically discriminable hypothesis. Its assessment need not rely solely on asymptotic reasoning, but may, in principle, proceed through observable indicators such as stability, resonance, and decoherence within an atemporal discriminator. While demonstrated here only through conceptual modeling and software simulation, this framework is explicitly designed to admit future physical realization, positioning RH as a prototype for reframing long-standing mathematical conjectures as experimentally accessible questions of structural admissibility.

References

Appendix 1: Python code for Figure 1

 
mp.dps = 35  # Increase if you want smoother/safer values (slower) 
EPS_MAG = 1e-40  # Prevent log(0) 
EPS_SCORE = 1e-12 
 
t_vals = np.linspace(14.1, 24.9, 60)          # t-grid 
sigma_vals = np.array([0.45, 0.50, 0.55])     # 3 curves for 2D figure 
 
zero_markers = [14.134725, 21.022040] 
 
def compute_neglog_zeta(sigmas, t_grid): 
    Z = np.zeros((len(sigmas), len(t_grid)), dtype=float) 
    for i, sigma in enumerate(sigmas): 
        for j, t in enumerate(t_grid): 
            s = mp.mpc(float(sigma), float(t)) 
            mag = float(abs(zeta(s))) 
            Z[i, j] = -np.log(max(mag, EPS_MAG)) 
    return Z 
 
print("Computing real zeta values for 2D figure...") 
Z = compute_neglog_zeta(sigma_vals, t_vals) 
 
# Full code available at the links below (Colab, GitHub, project website).

Appendix 2: Python code for Figure 2

 
mp.dps = 35 
EPS_MAG = 1e-40 
EPS_SCORE = 1e-12 
 
t_vals = np.linspace(14.1, 24.9, 50) 
sigma_vals = np.linspace(0.45, 0.55, 13)  # centered around 0.5 for ridge visualization 
 
def compute_neglog_zeta_grid(sigmas, t_grid): 
    Z = np.zeros((len(sigmas), len(t_grid)), dtype=float) 
    for i, sigma in enumerate(sigmas): 
        for j, t in enumerate(t_grid): 
            s = mp.mpc(float(sigma), float(t)) 
            mag = float(abs(zeta(s))) 
            Z[i, j] = -np.log(max(mag, EPS_MAG)) 
    return Z 
 
print("Computing real zeta surface...") 
Z = compute_neglog_zeta_grid(sigma_vals, t_vals) 
 
# Full code available at the links below (Colab, GitHub, project website).

Appendix 3: Python code for Figure 3

 
def step1_input_riemann_deepwell(param_range, t_vals, alpha=6.0, q=2.0, eps_floor=1e-6): 
 
    S, T = np.meshgrid(param_range, t_vals) 
    Z = zeta(S + 1j * T) 
 
    mag = np.abs(Z) + eps_floor 
 
    g = np.exp(-alpha * mag) 
 
    thr1 = np.quantile(g, 0.995) 
    x1 = (g >= thr1).astype(np.uint8) 
 
    g2 = g ** q 
    thr2 = np.quantile(g2, 0.990) 
    x2 = (g2 >= thr2).astype(np.uint8) 
 
    return x1, x2 
 
def step2_cjm_core_engine(x1, x2, gate="OR", beta=20.0, mode="logistic"): 
    x1_prev = np.roll(x1, shift=1, axis=0) 
    x1_prev[0, :] = 0 
    if gate == "MAJ": 
        clauses = ((x1 + x2 + x1_prev) >= 2).astype(np.uint8) 
    elif gate == "AND3": 
        clauses = (x1 & x2 & x1_prev).astype(np.uint8) 
    else: 
        clauses = (x1 | x2 | x1_prev).astype(np.uint8) 
    sat_density = clauses.mean(axis=0) 
 
# Full code available at the links below (Colab, GitHub, project website).