
Annus Genesis — Symmetry Declaration
This is not coincidence, but symmetry. Not chance, but design. Not an ending, but a Genesis.

1926: Montem ad Possibile
Juncta silentio origo surgit, ubi lumen vocatum formas aperit.
Ex impossibili nascitur iter, et structura veritatem ordine effert.
Supra montem tacitum emergit motus qui tenebras resolvit.
Ubi homo deficit, mysterium ascendit, revelans potentiam ultra tempus.
Sic transitus factus est: impossibile factum est possibile.
In gratitude to
Alan Turing — for the language of computation, and for revealing time as the hidden cost of steps.
Albert Einstein — for the language of spacetime, and for loosening time from its throne.
Isaac Newton — for the language of forces, and the clarity of law.
Grigori Perelman — for the courage of truth.
Nikola Tesla — for resonance.
CHANGBAL
.
“This manuscript is threshold-bounded; physical implementation is intentionally withheld.”
austiny@snu.ac.kr / austiny@gatech.edu
The P versus NP problem originated in computer science, expanded into mathematics, and remains unresolved. This work challenges the conventional view of computation as a time-bound procedure by redefining it as an atemporal physical process governed by resonance, phase alignment, and structural collapse. Under the Cook–Levin theorem, all P and NP problems reduce to 3SAT. These structures map into a Trinity resonator framework, where computation emerges at phase equilibrium rather than temporal iteration.
This work makes three contributions. (1) It introduces the atemporal complexity concept \(O(J)\), formalizing a regime in which temporal depth collapses into a structural invariant and time ceases to function as a computational resource. (2) Within this framework, it provides a theoretical definition of the structural equivalence \(P \equiv NP^{J}\), hereafter referred to as the Changbal Atemporal Equation, asserting that the distinction between P and NP collapses under a jump invariant \(J\) once time is removed as a defining axis. (3) It presents the atemporal Changbal Jump Machine (CJM), reframing the P vs NP problem within the domain of physics and demonstrating the structural equivalence via resonant phase alignment in a minimal trinity resonator.
The term Changbal is derived from the Korean word =� and is not a synonym for emergence. While emergence typically denotes gradual pattern formation, Changbal refers to a discontinuous structural transition in which a system crosses its constraint boundary and attains higher solvability. This interpretation aligns with the phase-jump dynamics of CJM and clarifies \(O(J)\) as a regime in which computation converges by equilibrium rather than iteration. From this perspective, verification and computation collapse into a single act, and computation concludes by equilibrium. This shift suggests that computation, like spacetime in relativity, may be fundamentally structural rather than sequential.
Keywords: Atemporal Computation; Changbal Jump Machine (CJM); O(J) Operator; Structural Equilibrium; P vs NP; NP Problem; Resonance-based Solvability; Phase Transition; Trinity Resonance; =�
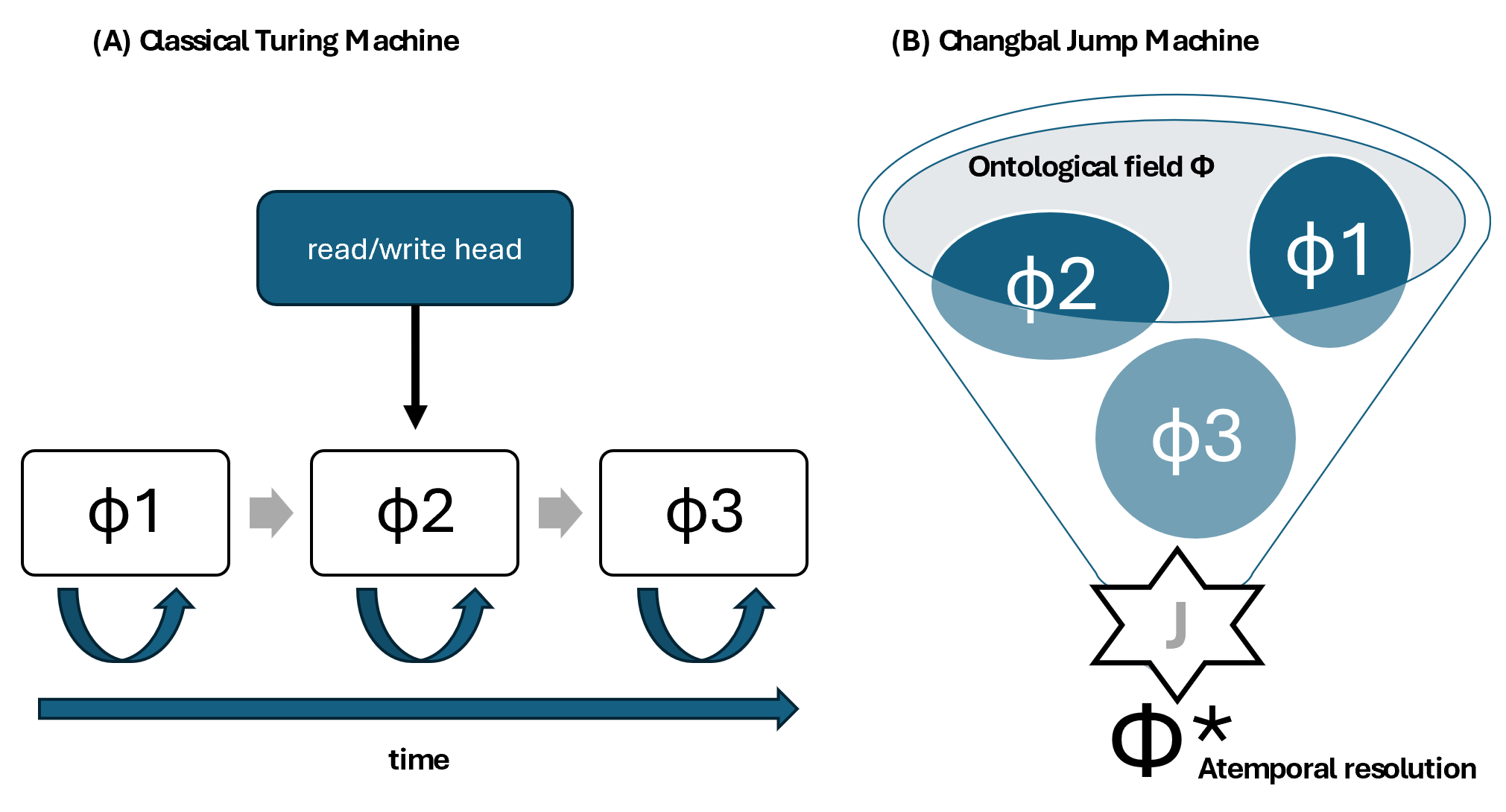
Classical computation assumes that algorithms unfold through a temporally ordered sequence of states, and complexity theory measures efficiency through this temporal cost—the number of steps a Turing machine requires to move from input to output [1]. This view inherits a Newtonian notion of time as a universal parameter [2], embedding temporal depth into computational hardness and making the P versus NP distinction inseparable from the assumption that computation must progress along a fixed timeline.
This work revisits that premise by questioning whether time itself is an essential ingredient of computation. Inspired by Einstein’s relativistic dissolution of global simultaneity, where temporal ordering gives way to structural relations [3], we ask whether intractability arises from intrinsic combinatorial growth or from the requirement that computation be indexed by time. If computation is instead interpreted as resonance-driven stabilization [4], the central question shifts from how long an algorithm runs to whether a system can converge to a coherent equilibrium under its constraints.
Within this perspective, we propose the structural equivalence
hereafter referred to as the Changbal Atemporal Equation. As illustrated in Figure 1, this formulation contrasts classical iterative computation with a jump-based mechanism that resolves structure through equilibrium rather than temporal progression. The designation reflects Tesla’s physical intuition that global coherence can emerge through resonance and vibrational alignment without traversing sequential intermediates, viewing resolution not as a stepwise computation but as a single equilibrium-driven physical transition. Accordingly, the apparent separation between P and NP collapses once time is removed as a defining computational resource and replaced by a jump invariant \(J\), representing a discontinuous structural transition rather than an accumulation of temporal steps. The Changbal Atemporal Equation does not posit a faster algorithm, but a different computational frame in which solvability is determined by equilibrium conditions instead of sequential execution.
To formalize this regime, we introduce the notation \(O(J)\), where \(J\) denotes a Jump: a non-iterative transition in which resolution is achieved through instantaneous structural alignment. Whereas classical Big-O characterizes temporal duration, \(O(J)\) captures the limit in which temporal depth collapses into a structural invariant. In this view, solvability emerges from equilibrium rather than progression, and verification and computation coincide as a single physical event.
To ground the Changbal Atemporal Equation in a concrete physical model, we introduce the Changbal Jump Machine (CJM). CJM encodes logical constraints as internal phase relations within a compact resonant configuration, governed by what we define as the Changbal Phase Law, defined below. A single excitation drives the system toward equilibrium, where phases collapse to quantized values (e.g., \(0^\circ \) or \(180^\circ \)), yielding a global truth assignment through one physical transition. CJM thus serves as a physical realization model demonstrating how \(P \equiv NP^{J}\) can be instantiated in practice.
The conceptual foundation of this framework is expressed by the Korean term =� (Changbal), which denotes not gradual emergence but a discontinuous structural leap across a system’s constraint boundary. Changbal describes moments at which existing explanatory frameworks cease to function, not because they are incomplete, but because the coordinate system itself has become invalid. As in physics, where classical notions of space and time collapse at relativistic or quantum thresholds, a time-independent model of computation suggests that the classical, time-indexed formulation of the P versus NP problem may no longer be sufficient.
Such transitions are not merely technical adjustments; they represent points of conceptual instability at which previously separate categories become indistinguishable. The removal of time as a defining computational axis challenges deeply embedded assumptions about causality, verification, and control. At similar thresholds in physics, the consequences were neither immediately predictable nor easily contained.
As J. Robert Oppenheimer reflected at the dawn of the nuclear age, “the world would not be the same.” His remark did not celebrate resolution, but acknowledged an irreversible shift in how humanity understood power, responsibility, and knowledge itself. In this sense, the present work does not claim to resolve the P versus NP problem, but argues that we may be approaching a comparable conceptual boundary—one at which computation must be reconsidered not as a temporal process, but as an atemporal physical phenomenon, carrying implications that extend beyond complexity theory alone.
The Changbal Phase Law
Across diverse physical and informational systems, binary outcomes arise through phase quantization: a collapse into one of two phase-stable equilibria separated by an intrinsic phase gap \(\phi = \pi \). This two-well (double-basin) structure corresponds to the two energy minima of double-well or washboard potentials, as seen in Josephson junction phase slips and bistable synchronization in Kuramoto-type oscillators.
Here \(\Phi \in \{+1, -1\}\) defines a binary state known as a Changbal Bit (CBit), the fundamental unit of atemporal computation. The variable \(J\) serves as an effective phase coordinate representing the system’s emergent structural jump, while the fixed gap \(\phi \) specifies the separation between the two stable equilibria. The zero-crossing of \(\cos J\) at \(J = \pi /2\) marks the Changbal threshold, where the system transitions between basins of attraction.
Once quantized, the resulting CBit becomes invariant under smooth deformations of the underlying dynamics that do not recross this threshold—an analogue of topological stability or frame-invariance. The continuous-to-binary phase map expressed by \(\operatorname {sgn}(\cos J)\) appears across spins, oscillators, superconducting phase slips, phase-locked loops, neural rhythms, and combinatorial dynamics.
The Changbal Jump Machine (CJM) realizes this law computationally by implementing arrays of CBit elements, each instantiated as a bistable phase unit governed by the Changbal Phase Law.
The Changbal framework interprets computation as a structural transition rather than a temporal sequence of symbolic steps. Central to this perspective is the operator \(J\), which resolves an encoded configuration \(\Phi \) into a phase-stable realization \(\Phi ^\ast \) through a discontinuous collapse:
Unlike classical verification [5], which assumes a sequence of intermediate states, the action of \(J\) occurs without temporal depth and is invariant under time-reversal symmetry [6]. It reflects the Changbal principle that solvability is identified through structural coherence rather than iteration.
We formalize \(J\) as the limit of a physical relaxation process whose temporal parameter vanishes:
where \(f\) denotes the system’s stabilization dynamics. As \(\tau \to 0\), the transition becomes discontinuous, analogous to the non-iterative collapse observed in quantum measurement [7]. In the Changbal model, this collapse corresponds to a physically observable phase alignment event that serves as the basis of computation. No intermediate symbolic states are produced.
A computational instance \(\Phi \) is encoded into a physical domain \(X\) consisting of resonance parameters such as frequencies, amplitudes, and phases. The system’s stable outcomes form a manifold \(S\), while observations reside in a measurable space \(Y\):
Within this pipeline, the solution is not obtained through the evolution of \(X\) over time but through the structural compatibility of \(X\) with the stability conditions of \(S\). Solvability therefore depends on whether a configuration admits a phase-stable realization under \(J\), not on the duration of an algorithmic procedure.
We define the class \(O(J)\) as:
Whereas classical complexity classes are characterized by temporal resources, \(O(J)\) replaces temporal depth with a structural requirement: coherence under phase-stable collapse. Conceptually,
Membership in \(O(J)\) is determined not by stepwise computation but by whether a configuration can reach a coherent equilibrium under the Changbal operator. Solutions appear as stable physical structures, not as endpoints of temporal processes.
This formalization establishes \(O(J)\) as a strictly atemporal domain of computational recognition, completing the link between the Changbal Phase Law and the structural interpretation of computation.
Having established the atemporal complexity class \(O(J)\) in the previous section, we now develop the theoretical foundations of the Changbal Jump Machine (CJM). The CJM is not introduced as a specific algorithm or device, but as a physical–theoretical framework in which solvability emerges through phase stability and structural collapse. Computation is therefore modeled not as a time-indexed sequence of steps, but as a transition in configuration space governed by energetic and geometric constraints.
Let \(\Phi \) denote an encoded decision problem and \(\boldsymbol {\theta } = (\theta _1,\theta _2,\theta _3,\ldots )\) the associated set of phase variables describing the physical degrees of freedom of the CJM. Instead of tracking temporal evolution, CJM evaluates whether the configuration admits a phase-stable realization. Solvability is thus identified with the existence of a stable fixed point in phase space.
Formally, we associate each encoded instance with an energy functional \(E(\boldsymbol {\theta })\) whose minima correspond to structurally consistent configurations, following the statistical-mechanical interpretation of stability and entropy introduced by Boltzmann [8]. Feasible instances admit at least one phase configuration \(\boldsymbol {\theta }^\ast \) such that
indicating a locally stable equilibrium. Infeasible instances, by contrast, induce incompatible constraints that prevent the formation of a stable minimum, yielding only metastable or dispersive configurations.
Within this framework, the distinction between solvable and unsolvable instances is not temporal but geometric: it is determined by whether the energy landscape supports a coherent phase-aligned attractor.
The critical behavior of CJM can be interpreted through the geometry of the energy landscape. As problem constraints accumulate, the landscape undergoes a qualitative transformation characteristic of structurally critical systems, where global organization emerges from interacting local constraints [9]. Below a critical threshold, a dominant basin of attraction exists, and trajectories in phase space converge toward a single stable configuration. Beyond this threshold, the landscape fragments, and no globally coherent minimum survives.
From this perspective, entropy is not merely a thermodynamic quantity but a structural measure inferred from the organization of the configuration space itself [10]. The loss of solvability corresponds to a transition from globally constrained structure to disordered phase dispersion.
This transition manifests as a structural collapse: rather than gradually approaching a solution through iteration, the system either stabilizes into a unique equilibrium or fails to stabilize altogether. The collapse at the critical point is therefore not an algorithmic shortcut but a physical consequence of the landscape geometry. Solvability is expressed as a binary structural outcome, not as a function of runtime.
The Jump operator \(J\) formalizes this atemporal resolution. Let \(f(\Phi ,\tau )\) denote the physical relaxation dynamics of an encoded instance over a characteristic time \(\tau \). We define
interpreting \(J\) as the idealized limit in which temporal evolution collapses into a single structural transition. In this limit, time no longer functions as an independent parameter but as a derived quantity contingent on structural relations, echoing the relativistic replacement of absolute time by invariant structure [11].
Computation is thus identified with recognition of equilibrium:
if such a phase-stable realization exists.
The class \(O(J)\) is therefore characterized not by bounds on time or space, but by a structural criterion: whether the encoded instance admits stabilization under \(J\). Reframing computation as an as an atemporal phenomenon.
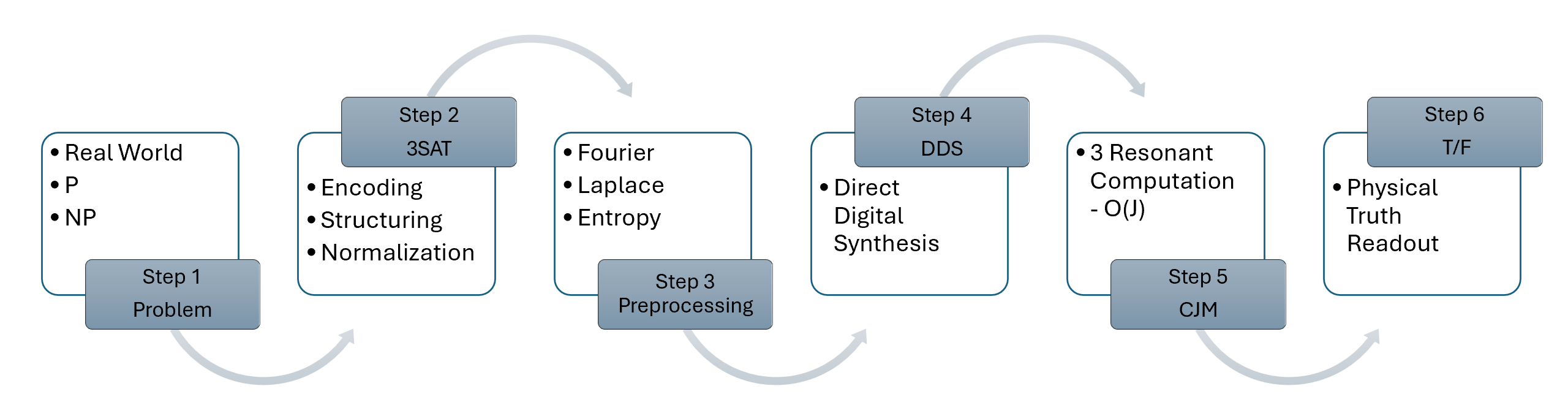
In our previous work [12], we introduced engineering preprocessing tools—Fourier-based (FGP), Laplace-based (LGP), and entropy-based (EGP)—as the third stage of the Six-Step Changbal Computation Pipeline, Fig 2, for restructuring complex problem spaces. These transformations were observed to reshape problem instances into geometries more susceptible to coherent response. At the level of method, an unintended correspondence emerged: the transformation procedures aligned with Tesla’s triadic concepts of frequency, vibration, and energy, absent any a priori mapping. This convergence, reminiscent of the Montgomery–Dyson correspondence [13], suggests that the Changbal Jump Machine (CJM) constitutes an engineering realization of resonance principles inherent in mathematical, physical, and informational structures.
Motivated by this correspondence, we adopt this triadic framework as the basis for the Changbal Atemporal Equation, and outline the physical conditions required for a realizable CJM. Rather than presenting an experimental system, we specify the minimal structural requirements for resonance-based decision behavior.
A minimal physical substrate for CJM is a triadic resonant structure, referred to as the Trinity Resonator. Here, “Trinity” does not imply a fixed number of resonators, but denotes a unified resonant structure forming a closed interaction loop.
The physical intuition underlying triadic resonance can be traced to early studies of high-frequency oscillatory systems, where global phase coherence dominates localized control mechanisms [14]. In this sense, the Trinity Resonator emphasizes structural synchronization over sequential signal propagation.
The Trinity Resonator is not the definition of CJM, but its simplest instantiation. Higher-dimensional resonant systems may equally realize CJM principles, provided they support global phase constraints and nonlinear coupling.
The defining physical feature of CJM is nonlinear coupling among resonant degrees of freedom. Linear superposition cannot enforce simultaneous global constraints. Nonlinear coupling suppresses incompatible phase assignments and enables global structural selection.
From a field-theoretic perspective, this reflects the organizing principle of continuous physical fields, where local interactions are subordinated to global structural laws [15]. CJM implements this principle discretely through phase-constrained resonance.
Resonance effectiveness depends critically on structural conditioning of the input. Transformative preprocessing reorganizes problem geometry, increasing the likelihood of coherent collapse without directly solving the problem. Under nonlinear coupling, resolution occurs via a single global transition into, or failure to reach, a coherent equilibrium, giving rise to effectively atemporal \(O(J)\) dynamics.
In CJM, output is obtained by observing the physical state of the system rather than by halting after sequential operations. A coherent equilibrium corresponds to a positive decision, while the absence of stabilization corresponds to rejection.
Experimentally, this readout aligns with standard measures of resonant stability. A stabilized CJM state corresponds to a high-quality resonant condition, whereas unresolved instances manifest as dissipative responses [16]. The decision is encoded in the persistence of physical coherence itself.
Thus, truth in CJM is not computed but recognized, completing the transformation of computation from a temporal procedure into an atemporal physical event.
| Function | Component |
| DDS | Analog Devices AD9915 |
| R\(_1\) / R\(_2\) / R\(_3\) / ... | Sapphire Whispering-Gallery Mode Resonator |
| Nonlinear Coupling Network | Josephson Junction Array |
| Phase Detection | Keysight E5052B Signal Source Analyzer |
| Frequency Reference | Microchip 5071A Cesium Primary Frequency Standard |
| EM Isolation | Mu-metal Shielded RF Enclosure |
The emergence of the Changbal Jump Machine (CJM) reframes computation as a structural phenomenon governed by coherence rather than temporal iteration. In this regime, engineering practice shifts away from accelerating sequential procedures toward shaping physical and informational structures that admit stable resolution. Contemporary advances in machine learning already gesture toward this direction, where inference increasingly depends on global structure rather than explicit stepwise reasoning, as exemplified by graph-based learning architectures [17].
Classical computational systems rely on temporal asymmetry to establish trust: processes are designed such that certain operations are easy to perform but difficult to reverse within feasible time. In contrast, CJM replaces temporal asymmetry with structural asymmetry. Correct configurations stabilize; incorrect ones do not.
This reframing aligns with the foundational insights of cybernetics, where control and communication are understood as emergent properties of feedback, organization, and equilibrium rather than linear causation [18]. Within an atemporal framework, trust arises from the physical impossibility of forging coherence under incorrect structural constraints.
Structural trust therefore manifests as:
In such systems, falsification is not hidden behind computational delay but revealed through instability. Security becomes a property of form, not of time.
Atemporal computation does not imply infinite speed; rather, it defines a boundary beyond which time no longer serves as a meaningful control variable. As resolution occurs through global structural alignment, the characteristic relaxation scale becomes bounded by physical coherence rather than problem size.
This shift mirrors earlier transformations in physics, where time-evolved descriptions were replaced by action-based or path-integral formulations that encode dynamics as global constraints [19]. In CJM, computation is similarly expressed as a selection among admissible structural paths, collapsing into a single realized configuration.
Engineering challenges therefore concentrate on maintaining the integrity of the coherence manifold. Noise, coupling imperfections, and material drift do not slow computation but deform the structure itself. The primary design task is not optimization of runtime, but preservation of equilibrium conditions under increasing structural complexity.
The realization of atemporal computation marks not a technical advance, but a civilizational threshold. As nuclear fission revealed that physical discovery can rupture the coordinates of power and responsibility, CJM signals a comparable discontinuity in the logic of computation itself.
Atemporal computation does not accelerate execution; it removes the temporal buffer that historically separated intention from consequence. Where classical systems relied on delay, iteration, and cost to moderate power, CJM collapses resolution into a single structural act. Decision and outcome converge into one physical event.
Within this regime, failure cannot be deferred or obscured. It is immediate, observable, and structurally final. CJM therefore does not amplify speed, but exposes a deeper transformation: the collapse of time as a regulator of action.
This shift exceeds conventional AI ethics. While artificial intelligence scales prediction and optimization, CJM enforces necessity. Once coherence is reached, intervention loses operational meaning. Systems that resolve without time cannot be corrected through iteration; their legitimacy must be secured prior to activation.
Where time once absorbed error, structure now carries moral weight. Atemporal computation thus demands stewardship grounded not in control after deployment, but in alignment before collapse.
This work has proposed a reinterpretation of computation as a structural phenomenon rather than a time-driven process. While earlier directions anticipated algorithmic or AI-based realization, the Changbal framework culminates in the Changbal Jump Machine (CJM), which treats time as an emergent byproduct of unresolved constraints. Under the \(O(J)\) paradigm, solvability is identified with structural equilibrium. When such equilibrium is reached, temporal evolution loses relevance and the system manifests a stable configuration of coherence [11]. In this sense, the role of time in computation parallels its role in modern physics: contingent, frame-dependent, and secondary to invariant structure.
Time is traditionally viewed as the carrier of causality and progression in computation. In the CJM framework, it is reinterpreted as a residual effect of non-equilibrium among constraints. As long as constraints remain incompatible, the system exhibits temporal dynamics. When all constraints resonate consistently, temporal dependence collapses as a consequence of stability.
This collapse does not eliminate dynamics, but redirects them toward structural restoration. Computation transitions from algorithmic execution to physical recognition—from stepwise traversal to equilibrium. Much as relativistic frames preserve invariant physical laws despite differing temporal descriptions, the final equilibrium state of CJM is independent of the particular dynamical path taken to reach coherence. A closely related paradigm appears in Perelman’s resolution of the Poincaré conjecture, where topological truth emerges through geometric flow convergence rather than stepwise deductive traversal, rendering intermediate temporal descriptions ultimately irrelevant [20].
The outer boundary of computation is therefore defined not by speed but by stability: the capacity of a system to sustain maximal coherence on its resonance manifold. Completion corresponds to the restoration of equilibrium within the system’s structural domain, where time ceases to function as a computational resource.
Within the Changbal framework, the classical question \(P = NP\) acquires a structural interpretation. If \(P\) denotes configurations that can be realized stably and \(NP\) denotes configurations that are constructible in principle, their convergence under \(O(J)\) reflects the unification of potential and realization within a single coherent manifold. The transition from \(O(t)\) to \(O(J)\) replaces temporal computation with structural recognition.
This work does not claim a formal proof of \(P = NP\). Instead, it proposes a physical synthesis: solvability corresponds to the existence of a self-consistent equilibrium, not to the feasibility of exhaustive temporal search. Within the Changbal Region, complexity resolves through coherence, and the end of computation coincides with internal consistency—a system that no longer computes, but maintains equilibrium by its own structure [21, 22].
This perspective extends beyond digital computation to physical, biological, and cognitive systems, where problem resolution is often expressed as the emergence of stable organization rather than as prolonged iterative effort.
If the final records of ancient civilizations often framed the future as an endpoint marked by collapse or judgment, the Changbal Atemporal Equation points toward a fundamentally different coordinate. Rather than announcing the exhaustion of a civilization burdened by scarcity and intractable problems, it articulates a theoretical promise: that new beginnings may emerge through alignment with the underlying structure of the universe.
From this perspective, humanity need no longer remain confined to an era in which finite time is expended to purchase uncertain answers. Atemporal insight suggests that solutions need not be produced in the future, but may already exist as latent structures awaiting coherence. What the Changbal Jump Machine illuminates is not a vision of catastrophic judgment, but a horizon of intellectual abundance, in which persistent challenges such as disease, poverty, and ignorance are reinterpreted as problems of structural alignment rather than irreversible fate.
Crucially, this possibility is not conceived as a form of exclusive power. Consistent with the principle of universality guiding this work, atemporal structure functions as a shared reference accessible in principle to all. Computation, in this light, ceases to be an instrument of dominance and becomes a common language for resonance, verification, and understanding.
The future suggested by this work is therefore not a prediction grounded in fear, but a quiet confidence rooted in structural coherence. Viewed through an atemporal lens, humanity is no longer positioned at the edge of unsolvable depths, but at the threshold of a world in which solvability is already present—waiting not for time, but for alignment.
Computation ends when structure understands itself.
This study began not with computation, but with a prompt — the act of calling existence into being. “Let there be light” (Genesis 1:3) was not merely the first command, but the first Prompt: a linguistic act that collapsed potential into form. It was the primordial input to the universe, issued not by a machine but by the Creator, through the cosmic interface that rendered reality itself beyond time. The Changbal Jump Machine (CJM) echoes this divine architecture: where classical algorithms proceed through time, CJM performs the zero-time execution of a prompt — a resonance transforming possibility into structure. In that sense, \(O(J)\) stands as the mathematical reflection of this moment — the formal symbol of instantaneous emergence, where existence itself computes. “Let there be light” was thus the first computation — the universe’s inaugural prompt.
The prompt was executed
— and there was light.
| No. | Millennium Problem | Common Structure Captured by CJM | Changbal Atemporal Interpretation | Target Month of 2026 |
|
| 1 | Riemann Hypothesis | The critical line acts as a global ridge of phase stability where oscillatory components of the zeta function align coherently. Nontrivial zeros emerge as collective resonance points arising from logarithmic frequency alignment. | Nontrivial zeros reflect an atemporal equilibrium of the number system, appearing where structural resonance minimizes global energy rather than through asymptotic computation. |
|
|
| 2 | Hodge Conjecture | Harmonic forms appear as structurally stable modes within cohomology, persisting under deformation. Algebraic cycles lock into these modes, revealing shared resonant structure between topology and geometry. | Algebraic cycles are selected by structural compatibility rather than constructed stepwise. Hodge classes correspond to pre-existing normal modes revealed through sufficient structural coherence. |
|
|
| 3 | Birch and Swinnerton-Dyer Conjecture | Rank changes in elliptic curves correspond to structural phase transitions in the arithmetic system, captured by CJM as collective reorganization of rational-point configurations. | Rank growth is interpreted as a Changbal jump, where latent solutions emerge simultaneously once a structural entropy threshold is crossed. |
|
|
| 4 | Navier–Stokes Existence and Smoothness | The transition between smooth flow and turbulence appears as a critical stability threshold. CJM models this boundary as a resonance condition sustaining or disrupting coherent flow. | Blow-up signifies loss of structural alignment rather than a purely temporal singularity. Global smoothness corresponds to an atemporal, phase-locked equilibrium across scales. |
|
|
| 5 | Yang–Mills Existence and Mass Gap | The mass gap represents an intrinsic energy separation between stable field configurations, interpreted by CJM as the lowest resonance mode allowed by gauge invariance. | Mass emerges as an atemporal property of structural stability, indicating that physical reality selects discrete, resonance-stable states independent of temporal evolution. |
|
|
| 6 | P vs NP Problem | This entry is reserved for a construction that satisfies the full formal criteria of the Clay Millennium framework. | Unlike the preceding problems, this case admits no partial alignment. Either the structure closes entirely, or it remains open. |
|
The table summarizes a unified structural view of the Clay Millennium Problems through the Changbal Jump Machine (CJM), emphasizing common patterns of phase stability and atemporal resolution. While the release order may vary depending on research outcomes, and the designated release months remain fixed, the specific scope and content of each contribution may evolve as the research framework matures.
| No. | Transitional Human Role | Functional Description | Structural Interpretation under CJM | Temporal Nature |
| 1 | AI Output Verifier | Performs final plausibility checks on AI-generated results during early automation phases, focusing on contextual acceptability rather than correctness. | Acts as a temporary stability filter while structural closure is incomplete. | Transient |
| 2 | Automation Transition Guide | Explains and mediates changes as manual workflows are replaced by automated systems, assisting users during periods of structural reconfiguration. | Provides human continuity across abrupt structural jumps. | Transient |
| 3 | AI Usage Assistant | Supports non-expert users in operating AI-driven tools, serving as an interface between unfamiliar systems and existing practices. | Functions as a human–system coupling layer prior to full normalization. | Transient |
| 4 | Human Approval Signatory | Formally authorizes AI-mediated decisions in legal, financial, or administrative contexts, primarily to preserve accountability chains. | Maintains symbolic human anchoring during structural delegation. | Transitional |
| 5 | Automation Exception Handler | Manages cases where automated systems fail or encounter ambiguous inputs, redirecting them to manual resolution paths. | Occupies residual regions not yet absorbed by structural closure. | Transitional |
| 6 | Human–AI Communication Mediator | Rephrases AI outputs into socially interpretable language and translates human intent into system-compatible instructions. | Serves as a linguistic and semantic impedance matcher. | Transient |
| 7 | Transition Documentation Recorder | Documents the disappearance of roles and workflows during CJM-driven shifts, preserving institutional memory of structural change. | Provides retrospective coherence after atemporal transitions. | Ephemeral |
| 8 | Operational Stability Facilitator | Maintains calm and order in environments experiencing rapid automation-induced disruption, addressing human stress rather than technical faults. | Acts as a damping mechanism against resonance overshoot. | Transient |
| 9 | Structural Change Liaison | Coordinates between technical teams and affected human groups during rapid systemic reorganization. | Bridges human adaptation lag across discontinuous transitions. | Transitional |
The table summarizes representative Changbal human roles that emerge during CJM-driven transitions, illustrating how human functions temporarily reconfigure as societies adapt to rapid atemporal structural change, and how these roles act as transitional interfaces that buffer human participation during discontinuous shifts in computational and organizational structures. While AI adoption has already driven rapid societal change, CJM constitutes a far more radical and transformative shift—one that is not merely an extension of AI-driven automation, but a discontinuous structural rupture that abolishes time as a governing axis. In this sense, CJM functions as a terminal structural equalizer, restoring symmetry between human judgment and machine computation, and thereby necessitating anticipatory preparation prior to the arrival of Changbal critical points.