Emergence in SAT Problems: Critical Thresholds under Constraint Density

Keunsoo Yoon

Independent Researcher | austiny@gatech.edu, austiny@snu.ac.kr

 

ABSTRACT

The SAT problem is a central NP-complete problem. This study experimentally explores whether a critical threshold—an emergence point—exists where the satisfiability of 3-SAT instances changes sharply as constraints increase.

By generating thousands of random instances and measuring satisfiability and solving time across varying constraint densities (r = m/n), we observed a phase-transition-like behavior. This approach offers a new perspective on NP problems, linking them with emergence phenomena in complex systems.

1 Introduction

The SAT(Satisfiability) problem asks whether there exists a variable assignment that satisfies a given logical formula. It is one of the most fundamental and significant decision problems in theoretical computer science. Particularly, SAT is the canonical NP- complete problem, and its central role in complexity theory stems from the fact that many other logical and mathematical problems can be reduced to it. Practically, SAT finds applications in various domains such as circuit verification, software testing, planning, and scheduling where the performance of SAT solvers often has a direct impact on real world systems.

The P vs NP problem, one of the most critical open questions in complexity theory, is closely tied to the structure of the SAT problem. If a general algorithm exists that can solve SAT instances in polynomial time, then all NP problems would likewise be solvable in polynomial time, implying P = NP. Therefore, SAT serves not merely as an isolated problem, but as a core experimental ground for the broader landscape of computational theory.

Traditional research on SAT has focused on algorithmic development, heuristic strategies, and backtracking optimizations. In parallel, theoretical approaches have sought to analyze the complexity and structure of the solution space. A particularly intriguing finding from experimental studies is that the satisfiability of SAT instances varies sharply depending on the ratio between the number of clauses and the number of variables, referred to as constraint density (r = m/n, where m is the number of clauses and n is the number of variables). This sudden change in satisfiability around a critical value resembles phase transitions in physics and shows structural similarity to emergence phenomena in complex systems.

Against this background, our study begins with the following question: As constraints accumulate in SAT problems, how does the structure that supports satisfiability collapse or emerge? Specifically, is there an actual emergence point— a critical constraint density— beyond which satisfiable solutions no longer exist? And can this point be quantitatively measured and mathematically modeled?

Based on this hypothesis, the present study experimentally investigates how the structure of the solution space evolves with increasing constraint density in SAT problems. We measure satisfiability and solving time across various values of n (the number of variables) while varying m (the number of clauses), aiming to observe whether there exists a range in which the probability of satisfiability rapidly decreases or converges to zero.

We interpret these findings not merely as an increase in computational complexity but as a qualitative transformation in the information structure itself. In other words, constraint accumulation does not just make the problem harder—it alters the topology of the solution space, effectively transforming it into a different kind of problem. This carries significant theoretical implications.

Lastly, this study draws interdisciplinary parallels by comparing the emergent behavior observed in SAT with similar patterns in other domains. Emergent systems in the humanities (e.g., language formation), cultural systems (e.g., emergence of norms), and big data (e.g., algorithmic singularities) all exhibit nonlinear and structural transformations once a certain threshold is crossed. These similarities suggest a broader, unified perspective through which we can understand the structure of information and computation systems.

2 Theoretical Background

The SAT(Satisfiability) problem is a decision problem that asks whether there exists an assignment of Boolean variables that makes a given propositional formula evaluate to true. It is typically expressed in Conjunctive Normal Form (CNF), where each clause is a disjunction of literals (connected by ∨), and the entire formula is a conjunction (∧) of such clauses. For example, in a formula like (x₁ ∨ ¬x₃ ∨ x₅) ∧ (¬x₂ ∨ x₄), the goal is to determine whether there exists a truth assignment to the variables x₁ through x₅ that satisfies the entire formula.

SAT was proven to be the first NP-complete problem by Cook's Theorem in 1971, and since then, numerous other problems have been polynomially reduced to SAT. As a result, SAT is widely regarded as a central model for understanding the structure of NP problems. Even restricted forms such as 3-SAT—where each clause contains exactly three literals—remain NP-complete, making it a standard format for complexity analysis and experimental study.

A key concept in the structure of SAT problems is the solution space. For n Boolean variables, there are 2ⁿ possible assignments. As n increases, the solution space expands exponentially. However, not all assignments are satisfying, and depending on the number and structure of constraints, the solution space may narrow significantly—or even vanish entirely.

Within this context, the constraint density—defined as r = m/n, where m is the number of clauses and n the number of variables—acts as a critical parameter in determining the behavior of SAT instances. Empirical studies have shown that below a certain threshold of r, most instances are satisfiable, whereas above this threshold, the probability of finding a solution drops sharply. This behavior mirrors phase transitions in statistical physics.

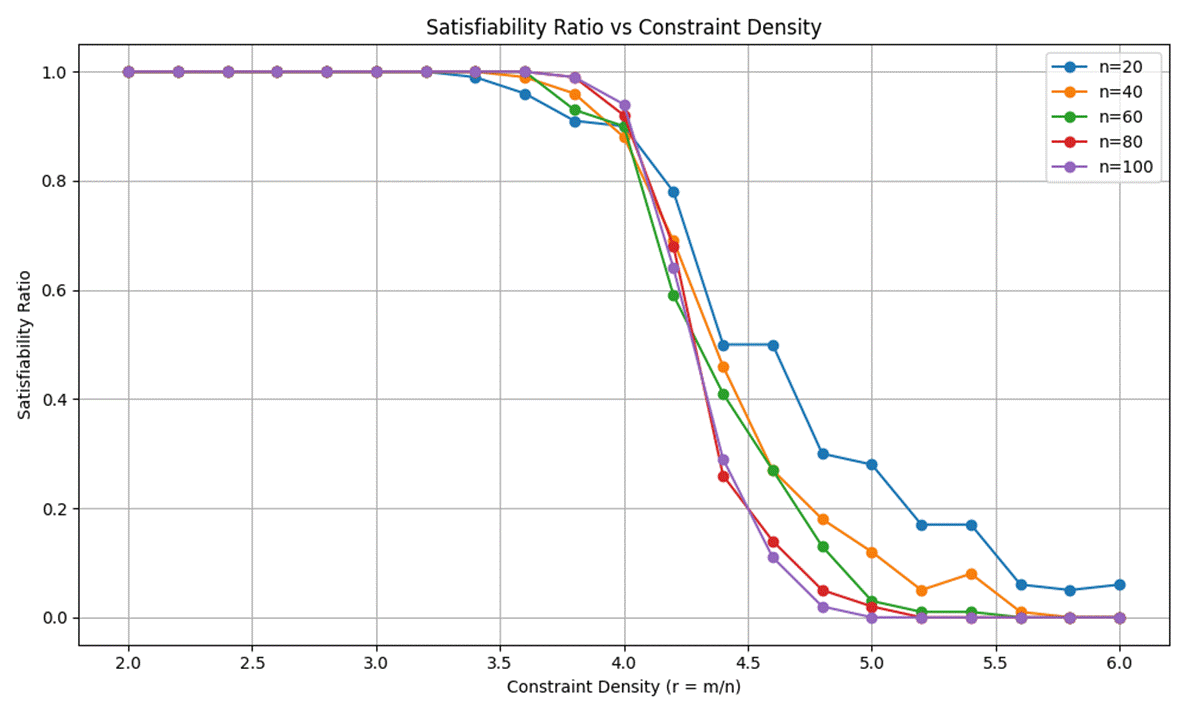
In particular, for 3-SAT problems, multiple studies report a sharp transition near r ≈ 4.26, beyond which satisfiable solutions become exceedingly rare. This indicates a structural shift in the formula space—from a regime rich in solutions to one where solutions nearly disappear. The phenomenon strongly suggests the presence of an emergence point or critical threshold, aligning with concepts discussed in complex systems theory.

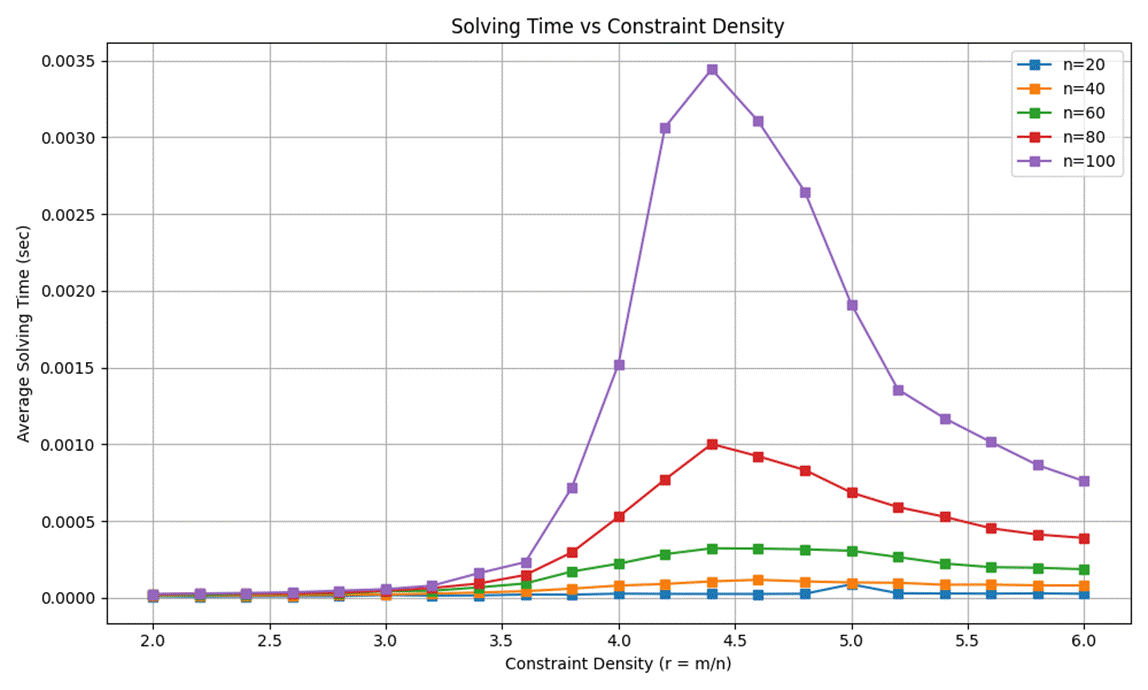
This phase transition is not merely about the presence or absence of solutions. It is also closely linked to the temporal and computational complexity of solving SAT instances. When the clause-to-variable ratio is very low, problems are easy to solve; when it is very high, unsatisfiability is quickly determined. However, near the critical point, the computational difficulty tends to peak. This has significant implications for SAT solver design and performance.

In summary, the SAT problem extends far beyond a simple decision problem. Its behavior changes nonlinearly depending on the amount and density of constraints, which in turn affects the structure of the solution space. This theoretical foundation provides a critical backdrop for the current study, which seeks to experimentally analyze the existence and characteristics of this emergence point.

3 Mathematical Modeling

The SAT problem can be seen as a combinatorial optimization problem over a discrete solution space. Understanding the structure of this space is essential for analyzing both the solvability and the computational complexity of the problem. In this section, we provide a mathematical formulation of SAT and outline the theoretical background for the existence of a phase transition based on constraint density.

A SAT instance consists of n Boolean variables and m clauses. Each variable can take a value of either true or false, resulting in a total solution space of size 2ⁿ. The core question is whether there exists an assignment that satisfies all clauses simultaneously.

In general, k-SAT problems, each clause contains exactly k literals, which are either variables or their negations. For example, a 3-SAT clause takes the form (x  ¬y  z). As more clauses are added, the valid region in the solution space becomes increasingly restricted, and the number of satisfying assignments decreases exponentially.

A key parameter that governs this behavior is the constraint density, defined as:

 

r = m / n

 

where m is the number of clauses and n is the number of variables. Lower values of r are typically associated with a high probability of satisfiability, while higher values sharply reduce the likelihood of finding a solution. In the case of 3-SAT, numerous studies report a sharp drop in satisfiability near the critical threshold rₐ ≈ 4.26.

This phase transition is not only about the presence or absence of solutions, but also about the computational difficulty. When r < rₐ, most instances are solved easily. Around r ≈ rₐ, solving time and algorithmic complexity tend to peak. For r > rₐ, unsatisfiability is often quickly determined.

The solution space can be conceptualized as a high dimensional discrete space of 2ⁿ binary vectors. Each clause excludes a specific region from this space. As constraints accumulate, the remaining space converges toward a function of the form:

 

          |S| <= 2 ^ n * P (r)

 

Here, |S| denotes the number of satisfying assignments, and P(r) represents the probability that a solution exists for a given constraint density r. Although the exact form of P(r) is analytically unknown, experimental results suggest it follows a sigmoid-like curve with a steep decline near the threshold.

Topologically, solutions are widely distributed in the space when constraints are sparse. As constraints increase, solutions begin to cluster, and near the critical point, these clusters lose connectivity. This phenomenon can be interpreted as a phase transition in the topological structure of the solution space, similar to what is observed in spin glass models in physics.

This theoretical modeling provides a foundation for the experimental analysis that follows. It helps explain how the accumulation of constraints reshapes the geometry and complexity of the SAT solution landscape.

4 Experimental Design

This section describes the experimental setup designed to empirically examine the relationship between constraint density r = m / n and the structure of the solution space, as  previously modeled. The objective is to observe whether a rapid transition in satisfiability occurs near a critical density threshold, and to analyze the corresponding variations in solving time and problem difficulty  quantitatively.

4.1 Variable Configuration

The main variables used in the experiments are as follows:

•        Number of variables (n): 20, 40, 60, 80, 100

•        Number of clauses (m): computed as m = floor(r × n)

•        Constraint density (r): increased from 2.0 to 6.0 in steps of 0.1

This configuration allows us to compare how the critical density and the contraction of the solution space shift as the size of n increases.

4.2 Instance Generation

For each combination of (n, r), 100 random CNF instances were generated in the standard 3SAT format. Each clause consists of three randomly selected variables from the total n, with each literal randomly negated with 50% probability.

The instance generation algorithm follows these steps:

1.   Define n Boolean variables.

2.   Compute m = ⌊r × n⌋ (the floor of r times n), and generate m clauses.

3.   For each clause, randomly select 3 distinct variables.

4.   For each variable, randomly decide whet-her to negate it (50% chance). The generated instances were saved in the DIMACS CNF format, which is directly compatible with SAT solvers.

4.3 SAT Solver and Execution Environm-ent

To measure satisfiability and solving time, we used the open source SAT solver MiniSAT. All experiments were conducted on Google Colab, a cloud-based platform. Due to potential variations in underlying hardware, the focus was placed on relative trends across constraint densities rather than absolute performance metrics. Each instance was given a maximum solving time of 60 seconds.

For each instance, the solver recorded two key metrics:

•        Satisfiability result (SATISFIABLE / UNSATISFIABLE)

•        Solving time (in seconds, up to a 60-second limit)

4.4 Repetitions and Statistical Processing

•        For each configuration, 100 instances were tested, and average values and standard deviations were calculated.

•        Satisfiability ratio was defined as the proportion of instances classified as satisfiable.

•        Solving time was averaged across all instances, regardless of satisfiability.

•        Critical point estimation was based on analyzing the satisfiability ratio curve as a function of r.

Additionally, the overall results were visualized using heatmaps, line charts, and variance plots, which are presented in detail in Chapter 5.

 

5 Experimental Results and Analy-sis

This chapter presents a comprehensive analysis of the data collected under the experimental framework described earlier. For each variable setting n = 20,40,60,80,100 random instances were generated and evaluated for each value of r, the constraint density. The results were statistically processed to analyze satisfiability ratios, solving times, and to estimate the critical threshold.

All related code and notebooks are accessible through the GitHub and Colab links in Appendix B.

Figure 1 Satisfiability Ratio vs Constraint Density.

5.1 Satisfiability Ratio Analysis

The primary metric is the satisfiability ratio, defined as the proportion of instances labeled SATISFIABLE by the solver. As r increases, this ratio gradually decreases from near 1 toward 0. In particular, consistent with previous studies on 3- SAT, the satisfiability probability sharply drops near r ≈ 4.2 ∼ 4.3, indicating a critical phase transition.

This observation aligns with the theoretical emergence point proposed earlier. The change in satisfiability is not linear but exhibits a sigmoid-like shape, which resembles phase transitions in physical systems.

As the constraint density (r = m/n) increases, the satisfiability ratio drops steeply near the critical region. The transition becomes more abrupt as the variable count n increases, indicating the emergence of threshold behavior.

For example, when n=20, the ratio drops from ~70% at r = 4.0 to below 25% at r = 4.4. When n = 60, the same range results in a drop from ~90% to under 5%, suggesting a sharper phase transition as the problem size grows. 

 

5.2 Solving Time Analysis

Solving time also varies non-linearly with respect to r:

•        For r < 3.5: most instances were solved quickly.

•        Near r ≈ 4.2: both average solving time and standard deviation increased significantly.

•        For r > 5.0: most instances were UNSAT and were rejected quickly, resulting in decreased solving time.

This suggests that the computational peak occurs near the critical density, where SAT solvers consume the most resources.

In particular, when n = 60, the average solving time peaked at approximately 0.0005 seconds near r = 4.2, while in other regions, it remained below 0.0001 seconds. This highlights the sharp rise in computational demand near the threshold.

For n = 100, the peak solving time also appears near r ≈ 4.3, reaching ~0.0035 seconds. Figure 2 confirms that the computational spike grows with problem size.

Figure 2 Solving Time vs Constraint Density.

The peak in average solving time occurs around the critical point r_c, where satisfiable instances transition to unsatisfiable ones. This spike reflects increased computational complexity in the boundary region.

5.3  Impact of Variable Count (n)

Although the overall trends remain consistent across different values of n, the location of the critical threshold converges as n increases. When n = 100, the critical region is tightly concentrated near r ≈ 4.26, which closely aligns with previous theoretical predictions.

Smaller values of n lead to smoother transitions, while larger values result in sharper shifts. For example, in the case of n = 100, the satisfiability ratio drops from 80% to 10% within a narrow range of r ≈ 4.16 ∼ 4.28, indicating both convergence of the critical point and the steepness of the transition.

5.4 Summary and Visualization Insights

The experiments clearly demonstrate that as constraint density r increases:

•        The satisfiability ratio drops sharply near the threshold.

•        Solving time peaks at the critical region.

•        These phenomena become more pronounced with larger n.

The accompanying visualizations — including satisfiability ratio plots, solving time curves, and heatmaps — support the hypothesis of a structural collapse in the solution space beyond a critical density. These results provide empirical evidence for phase transition behaviors in SAT problems and form the basis for the integrative discussion on emergence and complexity that follows in Chapter 6.

6  Interdisciplinary Interpretation and Emergent Structure

The previous chapter showed that both the satisfiability of SAT problems and their solving times change drastically at a specific threshold of constraint density r. This suggests not merely an issue of computational complexity, but a structural phase transition in the solution space itself. Such transitions exhibit strong similarities to phase transitions in physics and emergent phenomena in complex systems theory.

In particular, the sharp contraction of the solution space observed around r ≈ 4.2 can be interpreted as a structural transition in which combinations of independent variables reach a certain density and cause the entire system to shift into a new phase. This is not just a matter of increased difficulty or longer computation time—it marks a point where the very identity of the problem transforms.

This structural behavior is echoed across multiple domains. For example, in linguistics, the emergence of grammatical rules; in cultural systems, the formation of social norms; in economics, collective behavioral shifts; and in biological evolution, the appearance of new species—all demonstrate a common pattern where the accumulation of individual elements beyond a critical threshold leads to the sudden emergence of a new order. These are hallmark characteristics of emergent systems.

In our SAT experiments, the accumulation of constraints altered the topological structure of the solution space, and at a specific point, a new “pattern” became manifest. This directly corresponds to what emergence theory describes as a “micro-to-macro transition,” or the moment when data becomes structure. Thus, the experiment presented in this paper is not merely about whether a computational problem has a solution, but can be interpreted as a mathematical demonstration of how the accumulation of information leads to qualitative transformation.

This approach establishes an interdiscip-linary bridge between computational theory, information science, complex systems, and the humanities. Departing from conventional step-by-step reasoning, the idea of capturing the moment when accumulated information reshapes reality offers a new method that may be applicable to analyzing various complex systems in the future.

Most importantly, this interdisciplinary approach is not just a theoretical proposition, but suggests the potential for a quantitative framework that connects computational theory with cultural, philosophical, and social systems. Accordingly, this study proposes a new direction for expanding the scope of computational theory through the experimental exploration of critical behavior in complex information systems.

7 Conclusion

This study experimentally investigated the potential existence of an emergence point in SAT (Satisfiability) problems, where solutions either appear or disappear as constraints accumulate. By generating and analyzing thousands of randomly constructed 3- SAT instances based on the number of variables n, the number of clauses m, and constraint density r=m/n, we observed that satisfiability and solving time changed sharply near a specific value of r. This phenomenon resembles phase transitions in physics and emergent phenomena in complex systems, suggesting that the solution space of computational problems may also exhibit critical structures.

The experimental results offer the following key implications:

•        When the constraint density r exceeds a certain critical threshold (approximately r ≈ 4.2), the probability of satisfiability drops dramatically, and the solving time reaches a peak before declining again.

•        As the number of variables n increases, this critical phenomenon becomes more pronounced, indicating that topological changes in the solution space become more sensitive to problem size.

•        These results suggest the potential for a new approach that analyzes the solution space quantitatively and topologically, proposing the feasibility of structural analysis beyond traditional algorithmic perspectives.

The significance of this study lies beyond a simple SAT experiment. It provides numerical confirmation that when information accumulates beyond a certain threshold, a qualitative structural transition can occur. This enables comparisons with emergent behaviors observed in complex systems, the humanities, and cultural systems, and implies that the analytical framework of computational complexity may be expanded through interdisciplinary integration.

However, this study has the following limitations:

•        First, the SAT instances used in the experiments were limited to randomly generated standard 3-SAT problems, and did not address structured or real- world problems.

•        Second, the mathematical definition of the critical point and theoretical modeling of topological changes remain limited, relying primarily on empirical estimation.

•        Third, the results may have been partially affected by the performance of the solver and the imposed time limits.

Future research may consider the following directions:

•        Extension to k-SAT, structured SAT, and real-world constraint-based problems

•        Mathematical definition and formal proof of the critical point

•        Topological analysis of solution space clustering using tools from algebraic topology

•        Diversification of generation models and integration with neural network- based predictive models

•        Theoretical connection with qualitative  transitions in humanities and social systems

•        Philosophical reflection  on the emergence of structure and meaning, and their interpretation, through computational complexity

This study proposes a new possibility for extending the scope of computational theory by experimentally investigating the critical behavior of complex information systems in a multidisciplinary context.

References

1.     Cook, S. A. (1971). The complexity of theorem-proving procedures. Proceedings of the 3rd Annual ACM Symposium on Theory of Computing (STOC), 151–158. https://doi.org/10.1145/800157.805047

2.     Mitchell, D., Selman, B., & Levesque, H. (1992). Hard and easy distributions of SAT problems. Proceedings of the Tenth National Conference on Artificial Intelligence (AAAI), 459–465.

3.     Kirkpatrick, S., & Selman, B. (1994). Critical behavior in the satisfiability of random Boolean expressions. Science, 264(5163), 1297–1301. https://doi.org/10.1126/science.264.5163.1297

4.     Gent, I. P., & Walsh, T. (1994). The satisfiability constraint gap. Artificial Intelligence, 81(1–2), 59–80. https://doi.org/10.1016/0004-3702(94)

90043-4

5.     Hogg, T., Huberman, B. A., & Williams, C. P. (1996). Phase transitions and the search problem. Artificial Intelligence, 81(1–2), 1–15. https://doi.org/10.1016/0004-3702(94)

90039-2

6.     Monasson, R., Zecchina, R., Kirkpatrick, S., Selman, B., & Troyansky, L. (1999).

Determining computational complexity from characteristic ‘phase transitions’.

Nature, 400(6740), 133–137. https://doi.org/10.1038/21910

7.     Odlyzko, A. M. (1987). On the distribution of spacings between zeros of the zeta function. Mathematics of Computation, 48(177), 273–308.

https://doi.org/10.2307/2007890

8.     Wolfram, S. (2002). A New Kind of Science. Wolfram Media.

9.     MiniSAT GitHub repository. https://github.com/niklasso/minisat

10.  PySAT toolkit documentation. https://pysathq.github.io/

 

 Appendix A. Python Code for Generating SAT Instances

 This appendix presents the Python script used in the experiment to generate random 3-SAT instances. Given the number of variables n and constraint density r, the code generates m = int(r × n) clauses, each with three literals, and outputs them in DIMACS CNF format.

 

import random

 

def generate_3sat_instance(n, r):

    """

    Generates a random 3-SAT instance.

    n: number of variables

    r: constraint density (number of clauses m = r * n)

    Returns: a list of clauses (each clause is a list of 3 literals)

    """

    m = int(r * n)

    clauses = []

 

    for _ in range(m):

        # Select 3 distinct variables

        vars = random.sample(range(1, n + 1), 3)

        clause = []

        # Generate literals with random negation

        for v in vars:

            # Add negation with 50% probability

            if random.random() < 0.5:

                clause.append(f"-{v}")

            else:

                clause.append(f"{v}")

 

        clauses.append(clause)

 

    return clauses

 

# Example usage

if __name__ == "__main__":

    n = 50

    r = 4.2

    clauses = generate_3sat_instance(n, r)

 

    # Print in DIMACS CNF format

    print(f"p cnf {n} {int(r * n)}")

    for clause in clauses:

        print(" ".join(clause) + " 0")

 

 

 

 

Appendix B. Python Code for Running the Experiment and Visualization 

Complete code for SAT generation, experiments, and plotting is available at:

- GitHub (permanent):

https://github.com/keunsooyoon/Algorithms/blob/main/Emergence_in_SAT_Problems.ipynb 

- Colab (interactive):

https://colab.research.google.com/github/keunsooyoon/Algorithms/blob/main/Emergence_in_SAT_Problems.ipynb

 

Note: The Colab link may expire or become inaccessible. Core code snippets are included below for reference.

 

# Install PySAT (only needed on Google Colab)

!pip install python-sat[pblib,aiger]

 

# Import required libraries

import random

import time

import numpy as np

import matplotlib.pyplot as plt

from pysat.solvers import Glucose3

from tqdm import tqdm  # For progress bar

 

# Experiment configuration

n_values = [20, 40, 60, 80, 100]       # Number of variables

r_values = np.arange(2.0, 6.1, 0.2)   # Constraint density (m/n)

instances_per_setting = 100             # Number of SAT instances per setting

 

# Dictionary to store experiment results

results = {}

 

# Function: Generate a random 3-SAT instance

def generate_3sat_instance(n, m):

    """

    Generates a random 3-SAT CNF instance with n variables and m clauses.

    Each clause contains 3 literals, with 50% chance of negation.

    """

    clauses = []

    for _ in range(m):

        vars = random.sample(range(1, n + 1), 3)  # Choose 3 distinct variables

        clause = []

        for v in vars:

            clause.append(-v if random.random() < 0.5 else v)

        clauses.append(clause)

    return clauses

 

# Run experiment for each combination of (n, r)

for n in n_values:

    sat_ratios = []   # Satisfiability ratio per r

    avg_times = []    # Average solving time per r

 

    for r in tqdm(r_values, desc=f"Running for n={n}"):

        m = int(r * n)       # Number of clauses

        sat_count = 0        # Number of satisfiable instances

        total_time = 0.0     # Total solving time

 

        for _ in range(instances_per_setting):

            cnf = generate_3sat_instance(n, m)  # Generate CNF

            solver = Glucose3()                 # Initialize SAT solver

 

            for clause in cnf:

                solver.add_clause(clause)

 

            start = time.time()

            sat = solver.solve()

            elapsed = time.time() - start

 

            if sat:

                sat_count += 1

            total_time += elapsed

 

            solver.delete()

       # Compute statistics for this (n, r) setting

        sat_ratio = sat_count / instances_per_setting

        avg_time = total_time / instances_per_setting

        sat_ratios.append(sat_ratio)

        avg_times.append(avg_time)

 

    # Save results for this n

    results[n] = {

        'r': list(r_values),

        'sat_ratio': sat_ratios,

        'avg_time': avg_times

    }

 

# Plot 1: Satisfiability Ratio vs Constraint Density

plt.figure(figsize=(10, 6))

for n in n_values:

    plt.plot(results[n]['r'], results[n]['sat_ratio'],

             label=f'n={n}', marker='o')

plt.xlabel("Constraint Density (r = m/n)")

plt.ylabel("Satisfiability Ratio")

plt.title("Satisfiability Ratio vs Constraint Density")

plt.grid(True)

plt.legend()

plt.tight_layout()

plt.savefig("satisfiability_ratio.png")

plt.show()

 

# Plot 2: Average Solving Time vs Constraint Density

plt.figure(figsize=(10, 6))

for n in n_values:

    plt.plot(results[n]['r'], results[n]['avg_time'],

             label=f'n={n}', marker='s')

plt.xlabel("Constraint Density (r = m/n)")

plt.ylabel("Average Solving Time (sec)")

plt.title("Solving Time vs Constraint Density")

plt.grid(True)

plt.legend()

plt.tight_layout()

plt.savefig("solving_time.png")

plt.show()